Determinantes de ordem maior ou igual a 4
Para o cálculo de determinantes de matrizes quadradas de ordem superior a 3 utiliza-se o teorema de Laplace, que estabelece o seguinte:
- O determinante duma matriz é igual à soma dos produtos dos elementos duma qualquer linha ou coluna pelos respetivoscomplementos algébricos.[1]
O complemento algébrico dum elemento ai,j duma matriz e o número  , sendo
, sendo  o determinante da matriz que se obtém eliminando da matriz original a linha i e a coluna j.
o determinante da matriz que se obtém eliminando da matriz original a linha i e a coluna j.
 , sendo
, sendo  o determinante da matriz que se obtém eliminando da matriz original a linha i e a coluna j.
o determinante da matriz que se obtém eliminando da matriz original a linha i e a coluna j.Na prática, isto equivale a reduzir o cálculo do determinante duma matriz de ordem n ao cálculo de determinantes de matrizes de ordem n-1. O Teorema de Laplace pode ser aplicado as vezes que forem necessárias até obter matrizes de ordem 2 ou 3, cujo determinante é mais facilmente calculado através da regra de Sarrus.
A escolha da linha ou coluna da matriz a que se aplica este processo é indiferente, contudo, para maior simplicidade dos cálculos, convém escolher a linha ou coluna que contiver mais zeros.
Exemplo
Seja a matriz
Desenvolvendo o determinante pela primeira linha obtemos:



 ,
,
onde A−i,−j representa a matriz obtida a partir de A, com a retirada da i-ésima linha e da j-ésima coluna. Retorna-se ao cálculo de quatro determinantes de matrizes de terceira ordem.
Então definimos o determinante de ordem n desenvolvido pela i-ésima linha:
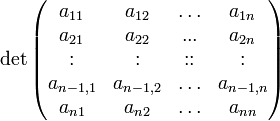
 .
.
Matrizes n por n
O determinante de uma matriz de tamanho arbitrário pode ser encontrado pela fórmula de Leibniz para determinante.
A fórmula de Leibniz para determinante de uma matriz A, n por n é
Cálculo de determinantes por triangularização
Tendo em vista a propriedade de que o determinante de uma matriz triangular é o seu termo principal (propriedade 5), a idéia é aplicar operações elementares sobre suas linhas, de modo a triangularizá-lo. Para isso devemos observar os efeitos que cada operação elementar pode ou não causar no valor do determinante procurado:
- Permutar linhas troca o sinal do determinante (propriedade 7);
- Multiplicar uma linha por um número real
 não nulo, multiplica o determinante por
não nulo, multiplica o determinante por  (propriedade 6);
(propriedade 6); - Somar a uma linha um múltiplo de outra não altera o determinante (propriedade 9).
Para triangularizar um determinante basta atentar para as possíveis compensações provocadas pelas operações elementares utilizadas e não há uma única maneira de realizar esse processo. O método é algorítmico, constituído de passos simples: a cada coluna, da primeira à penultima, deve-se obter zeros nas posições abaixo da diagonal principal. Veja o exemplo a seguir:

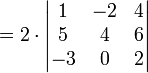








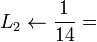

 de ordem
de ordem  , é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem
, é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem ![M=[a_{11}] \,](http://upload.wikimedia.org/wikipedia/pt/math/4/8/1/481b64913d043bcb7db7990f67b80854.png) temos que o determinante é o número real
temos que o determinante é o número real 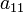 :
: .
. , então
, então  .
.
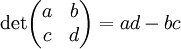 .
. é dado por:
é dado por:  .
.
 .
.
