Matriz (Parte 2)

Matriz identidade

A matriz identidade I_n é a matriz quadrada n × n em que todas as entradas da diagonal principal são iguais a 1 e as demais são iguais a zero, por exemplo

.

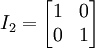Ela é chamada de matriz identidade pois multiplicá-la por outra matriz não altera a matriz: MI_n = I_mM = M para qualquer matriz M de ordemm por n.

Matriz inversa

Uma matriz A ^{− 1} é dita inversa de uma matriz A, se obedece à equação matricial A.A ^{− 1} = I, ou seja, se o produto entre as matrizes é amatriz identidade. A analogia com os números reais é evidente, pois assim como o produto entre dois números inversos é a unidade (elemento neutro da multiplicação), o produto entre duas matrizes inversas é a matriz identidade (elemento neutro da multiplicação entre matrizes). Uma matriz que possui inversa é dita inversível.

A condição necessária e suficiente para que uma matriz quadrada seja inversível é possuir um determinante não nulo, sendo que para uma dada matriz A, a matriz inversa é única. A necessidade de possuir determinante não nulo é evidente na equação , pois nela o determinante da matriz original é denominador de uma fração.

Matriz transposta

A matriz transposta de uma matriz A_{m × n} é a matriz A^t_{n × m} em que , ou seja, todos os elementos da primeira linha, tornar-se-ãoelementos da primeira coluna, todos os elementos da segunda linha, tornar-se-ão elementos da segunda coluna, todos os elementos da nlinha, tornar-se-ão elementos da n coluna. Exemplo:

Matriz simétrica

Uma matriz A é simétrica se A = A^t. Isso só ocorre com matrizes quadradas.

Um tipo especial de matriz simétrica é a matriz idempotente.