Determinante de uma matriz de ordem 1
O determinante da matriz 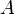 de ordem
de ordem  , é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem
, é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem ![M=[a_{11}] \,](http://upload.wikimedia.org/wikipedia/pt/math/4/8/1/481b64913d043bcb7db7990f67b80854.png) temos que o determinante é o número real
temos que o determinante é o número real 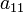 :
:
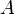 de ordem
de ordem  , é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem
, é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem ![M=[a_{11}] \,](http://upload.wikimedia.org/wikipedia/pt/math/4/8/1/481b64913d043bcb7db7990f67b80854.png) temos que o determinante é o número real
temos que o determinante é o número real 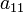 :
: .
.
Por exemplo:
 , então
, então  .
.Determinante de matriz de ordem 2
O determinante de uma matriz de segunda ordem é a diferença entre o produto dos termos da diagonal principal e o produto dos termos da diagonal secundária. Esses produtos se chamam, respectivamente, termo principal e termo secundário da matriz.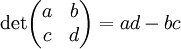 .
.
Por exemplo, o determinante da matriz é dado por:
é dado por:  .
.
Determinante de matriz de terceira ordemPara calcular o determinante de matrizes de terceira ordem, utilizamos a chamada regra de Sarrus, que resulta no seguinte cálculo: .
.
- Por exemplo:




Nenhum comentário:
Postar um comentário